SRCNN
Introduction
It is a re-implementation of paper named “Learning a Deep Convolutional Network forImage Super-Resolution” called SRCNN model. Training codes and applying codes are provided based tensorflow.
Network proposed
The LR input is firstly bicubic interpolated into a HR-sized image, then normal feature extraction, mapping and reconstruction are used. The network here is aimed at learning the mapping relationship between bicubic interpolated image and real image.
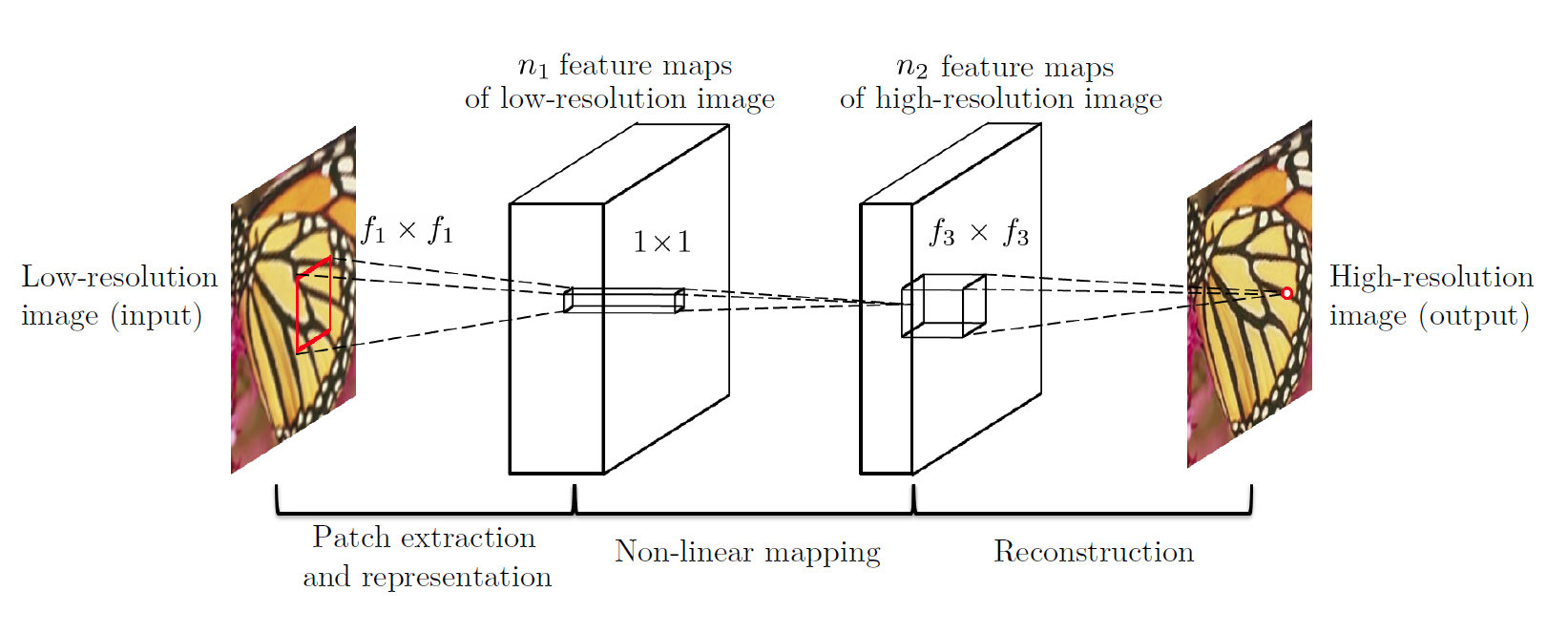
Analysis of Network
As the table shows below, it is bicubic-interpolation used too much resources that limits the time performance of this model.

Methods of Interpolation
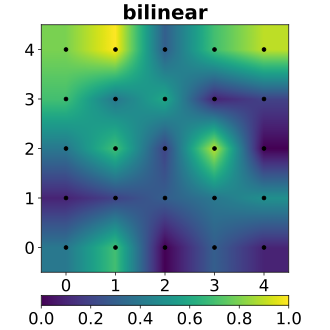
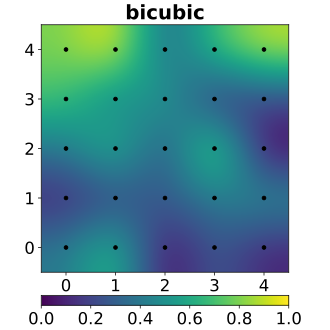
Bilinear Interpolation
Bilinear interpolation produces a smoother interpolation than does the nearest neighbor approach. Given four neighboring image coordinates \(f(n_{10},n_{20}),f(n_{11},n_{21}),f(n_{12},n_{22}),f(n_{13},n_{23})\) (these can be the four nearest neighbors of $f[a(n)])$, then the geometrically transformed image $g(n1, n2)$ is computed as \(g(n_1,n_2)=A_0+A_1n_1++A_2n_2++A_3n_1n_2\) which is a bilinear function in the coordinates $(n1, n2)$. The bilinear weights $A_0$, $A_1$, $A_2$, and $A_3$ are found by solving \(\begin{bmatrix} A_0 \\ A_1 \\ A_2 \\ A_3 \end{bmatrix} = \begin{bmatrix} 1 & n_{10} & n_{20} & n_{10}n_{20} \\ 1 & n_{11} & n_{21} & n_{11}n_{21} \\ 1 & n_{12} & n_{22} & n_{12}n_{22} \\ 1 & n_{13} & n_{23} & n_{13}n_{23} \end{bmatrix} ^{-1} \begin{bmatrix} f(n_{10},n_{20}) \\ f(n_{11},n_{21}) \\ f(n_{12},n_{22}) \\ f(n_{13},n_{23}) \end{bmatrix}\) Thus, $g(n1, n2)$ is defined to be a linear combination of the gray levels of its four nearest neighbors. The linear combination defined by above is in fact the value assigned to $g(n1, n2)$ when the best (least squares) planar fit is made to these four neighbors. This process of optimal averaging produces a visually smoother result.
Bicubic Interpolation
Bicubic Interpolation can be calculated by below \(f(x,y)=a_{00}+a_{10}x+a_{01}y+a_{11}xy+a_{02}y^2+a_{21}x^2y+a_{12}xy^2+a_{22}x^2y^2+a_{30}x^3+a_{03}y^3+a_{31}x^3y+a_{13}xy^3+a_{32}x^3y^2+a_{23}x^2y^3+a_{33}x^3y^3\)
This formula can be written by another form \(f(x,y)=\sum_{i,j=0}^3a_{ij}x^iy^j\) Since there are 16 parameters in the formula, the calculation of Bicubic Interpolation relays on the surrounding 16 values of points. It means we need to do 16-dimensional matrix operations at least once per pixel. The calculation of parameters and interpolation of pixels are essential.
Step 1: The calculation of parameters \(A=Var^{-1}f(x,y)\) Step 2: The interpolation \(f(x,y)=Var·A\) where $A$ stands for parameters, $Var$ stands for the variables in formulas ($x^iy^j$), $f(x,y)$ represents the value of points surrounding.
Results
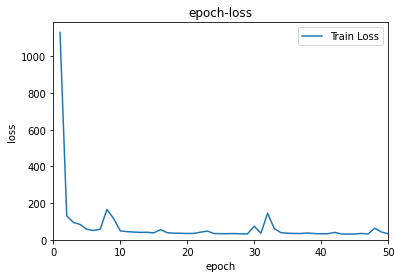
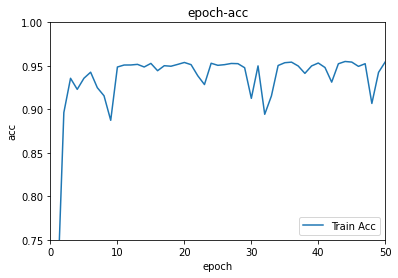
After 50 epoches, the model performs not bad on train data.
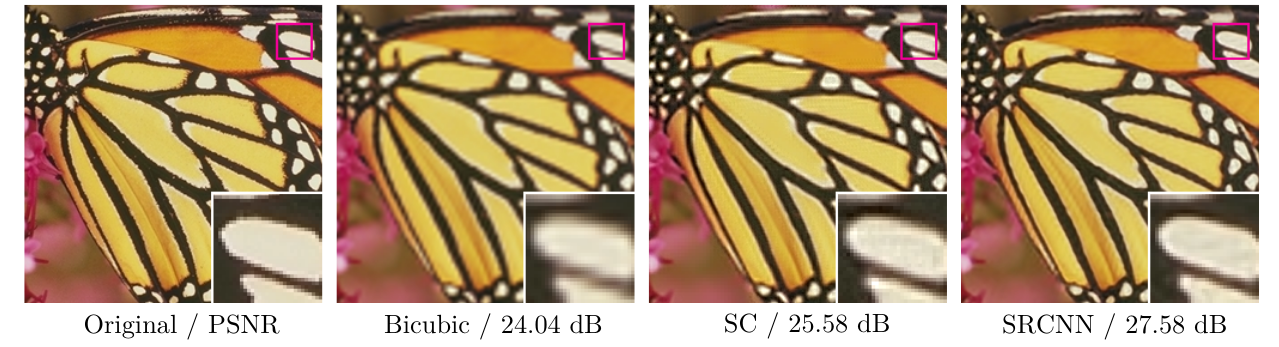
The SRCNN has a better result than traditional method about SR problem, as the Figure shows below (original from paper).
Author
Wenkang Zhu
If you have or find any problems, this is my email: wenkang_zhu@whu.edu.cn. And I’m glad to reply it. Thanks.
Reference
- https://www.sciencedirect.com/topics/computer-science/bilinear-interpolation
- https://wikimili.com/en/Bicubic_interpolation
- 双三次插值