高数占整个数学一考研的56%，属于数学一的基本盘。

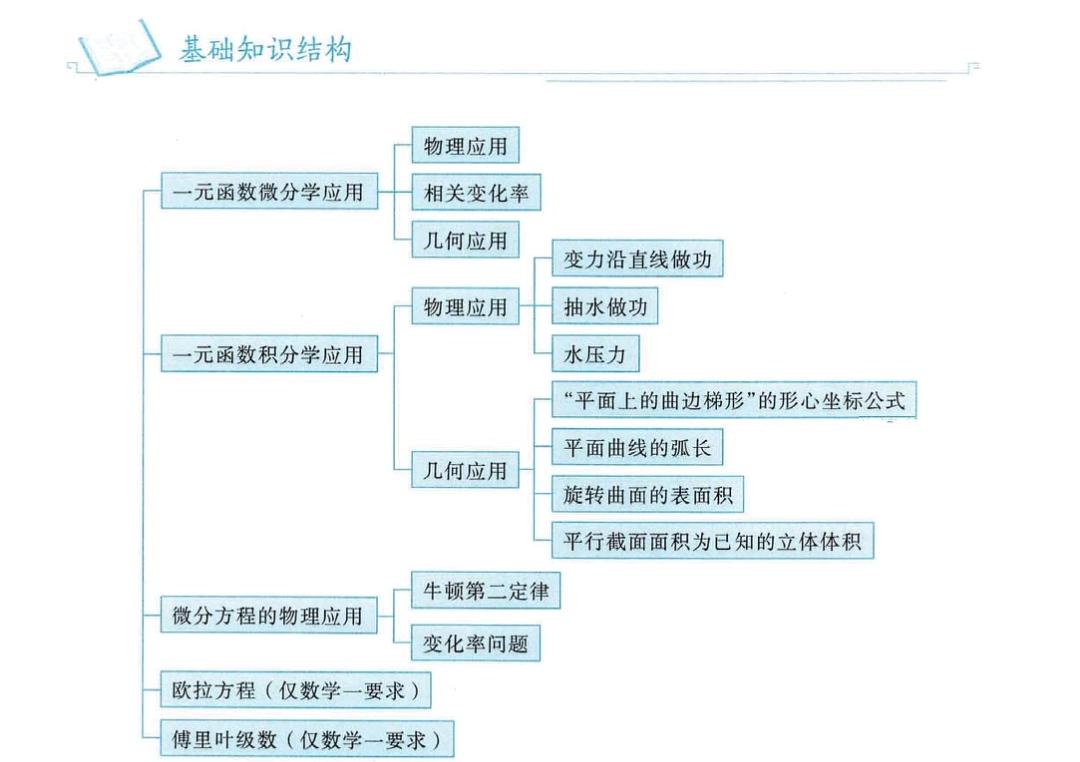
第11讲 多元函数微分学

P157-170，这一讲概念比较多，东西比较杂，但是内容不难，计算量比较大。

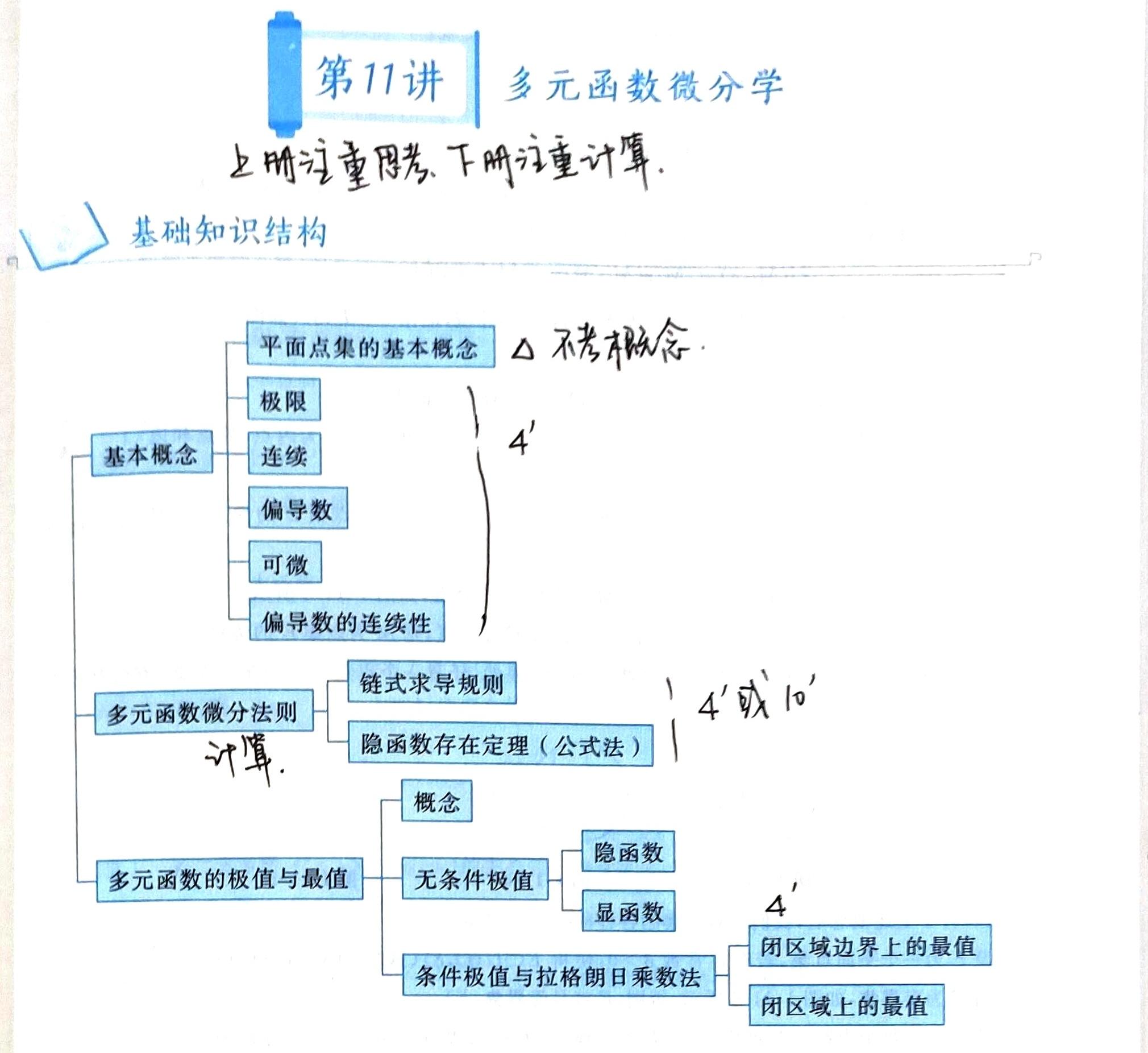
第12讲 二重积分

二重积分原理上不太难，但是需要掌握几个要点。

• 几何意义
• 对称性，其中轮换对称性还比较重要
• 直角坐标和极坐标的互化
• 积分次序的变更
• 用二重积分解决一元积分问题

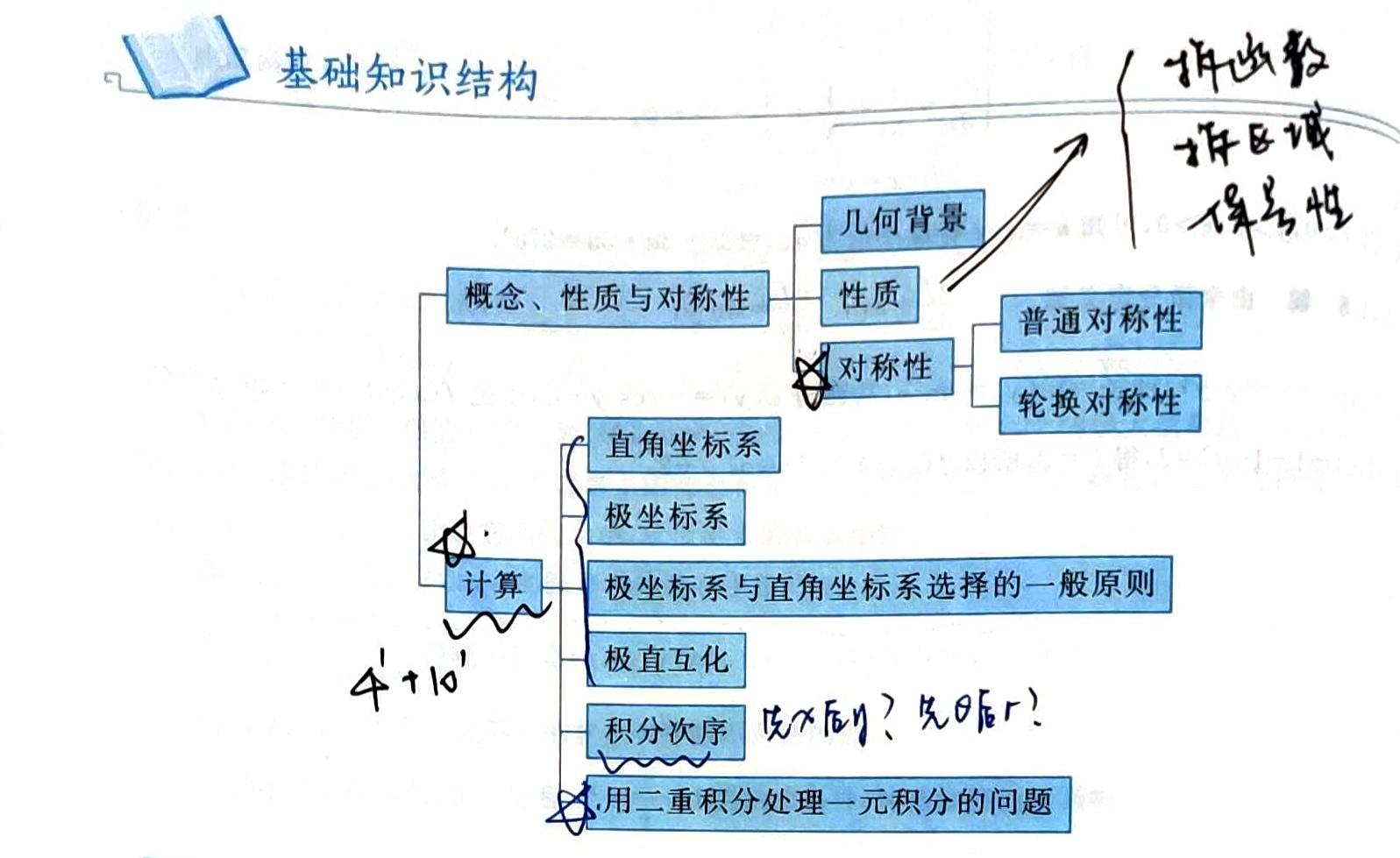
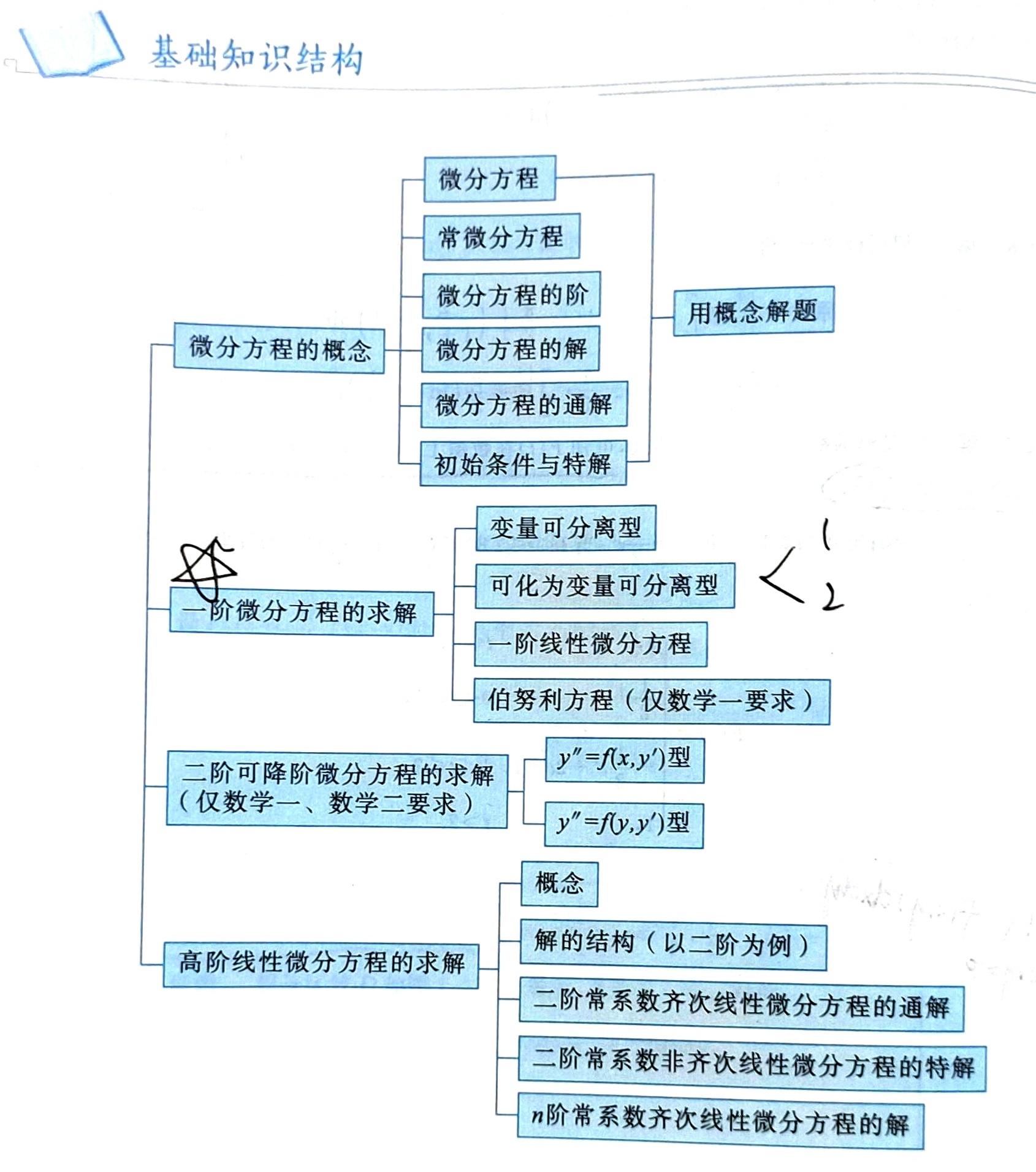
第13讲 常微分方程

这一章要背的好多，主要是各种微分方程的通解和特解。最好把一阶的和二阶的区分开背，这样可能比较简单。
计算的时候用到不少常见的积分和微分等式。

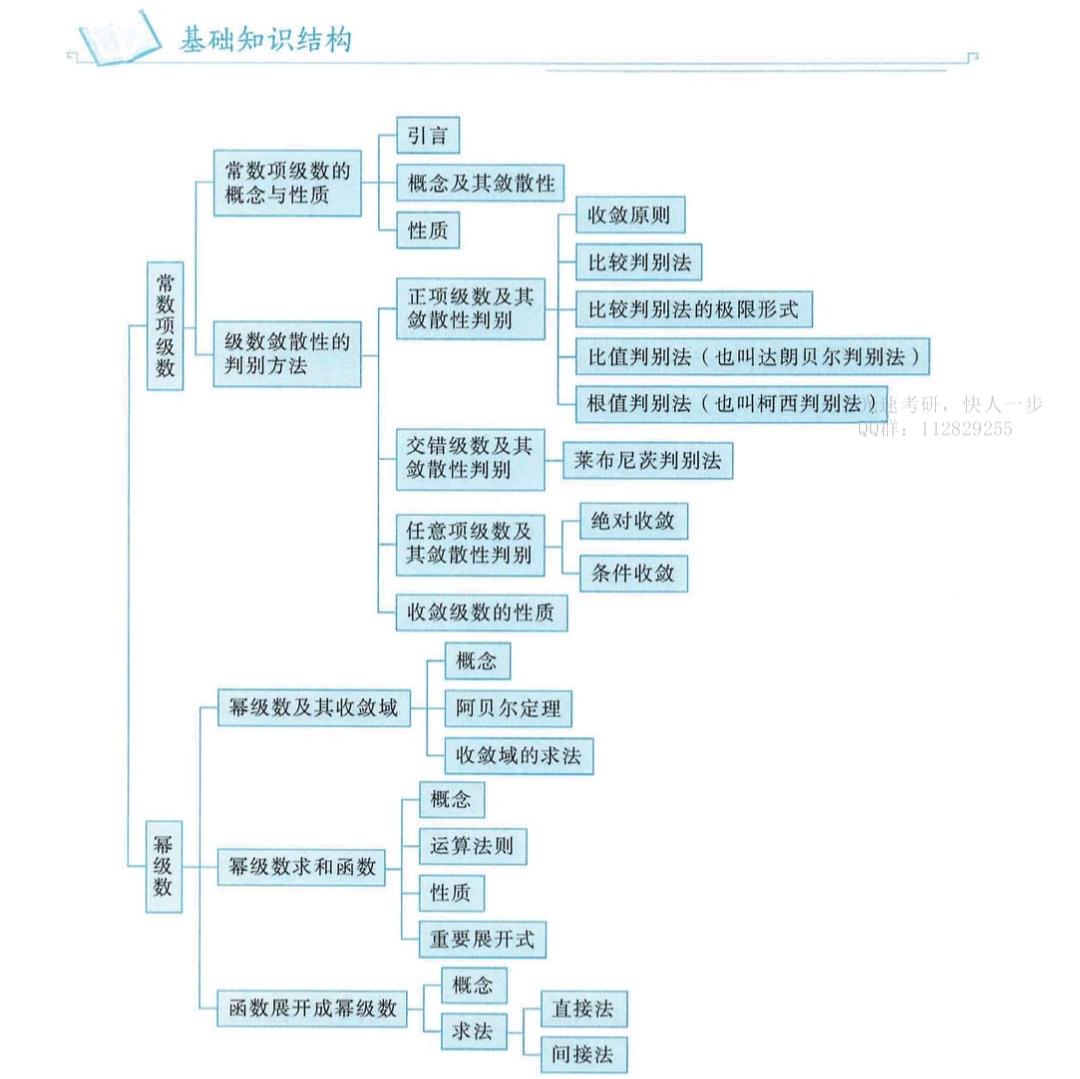
第14讲 无穷级数

这个很难，需要重点复习。考点有：

• 正项级数及其敛散性（达朗贝尔和柯西）
• 交错级数及其敛散性（莱布尼茨判据）
• 任意项级数及其敛散性
• 幂级数（阿贝尔和收敛域）
• 幂级数求和、函数展开为幂级数

经验：

• 7个常见的重要展开式及收敛域（麦克劳林展开）
• 调和级数，交错调和级数，p级数等常见级数
• 不等式公式有一些会用在敛散性证明的构造上
• 幂级数求和常用逐项求导或逐项积分

第15讲 数一应用题

闭关第1天：完成第15讲，主要讲的是数学一应用题，欧拉公式和傅立叶级数。

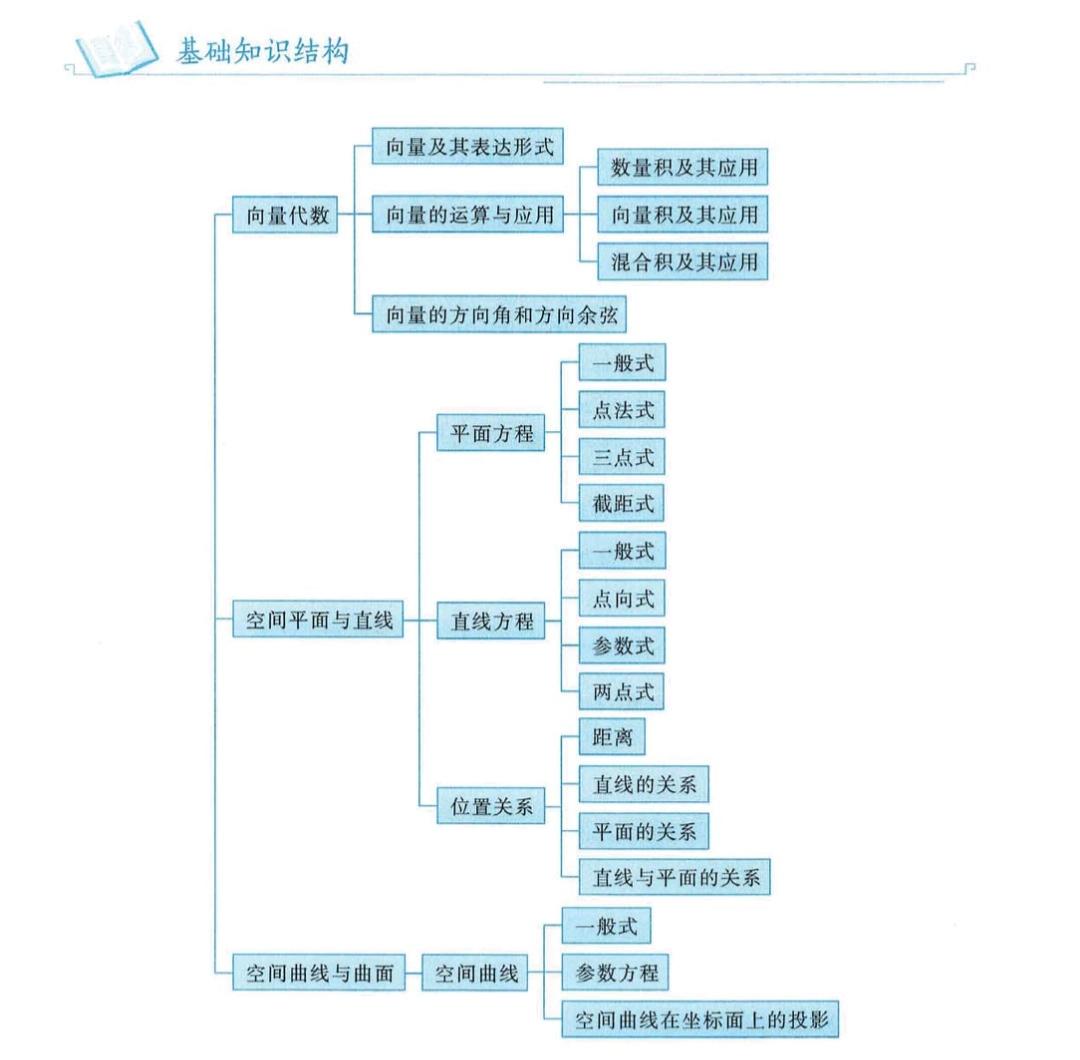
第17章 多元函数积分学的基本知识

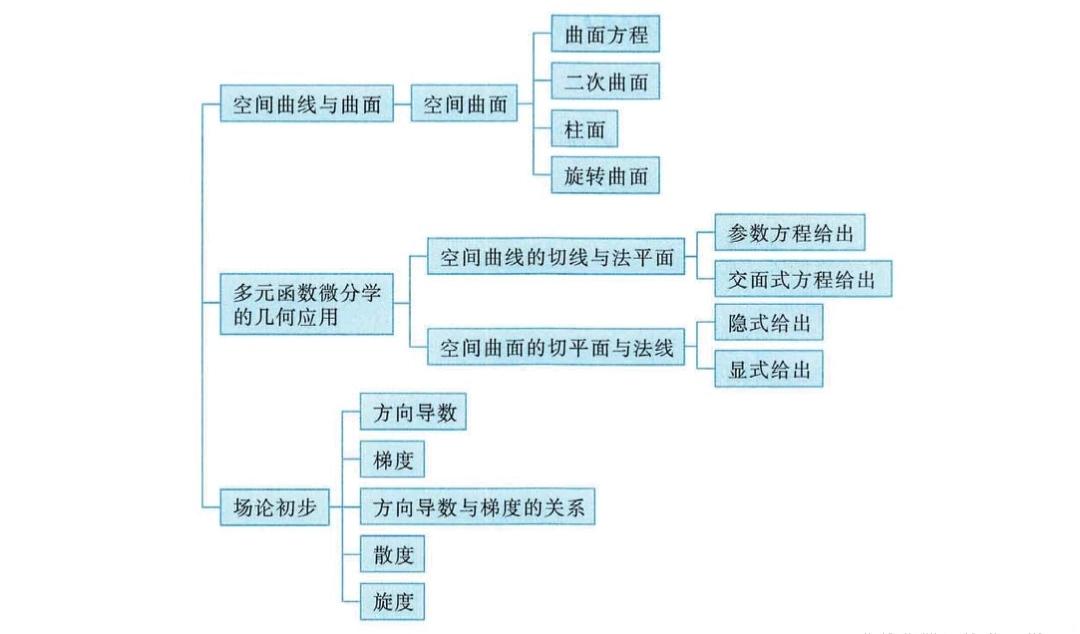
这讲也是多元函数微积分的应用题，涉及到空间解几问题。需要背好的有：

• 空间旋转曲面的求法
• 空间曲面的切平面和法线
• 空间曲线的切线和法平面
• 方向导数与梯度
• 散度和旋度

散度和旋度的物理意义是什么？.pdf

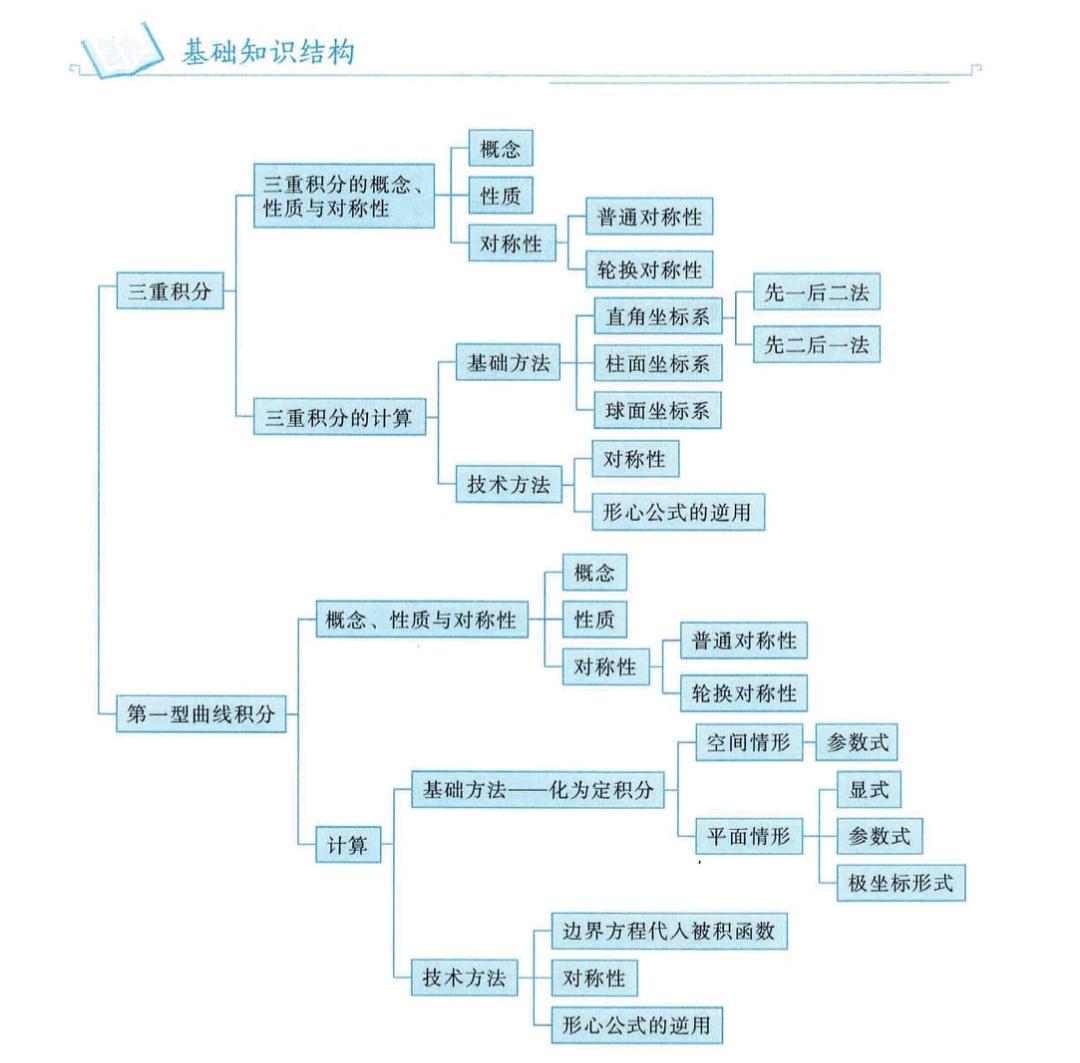
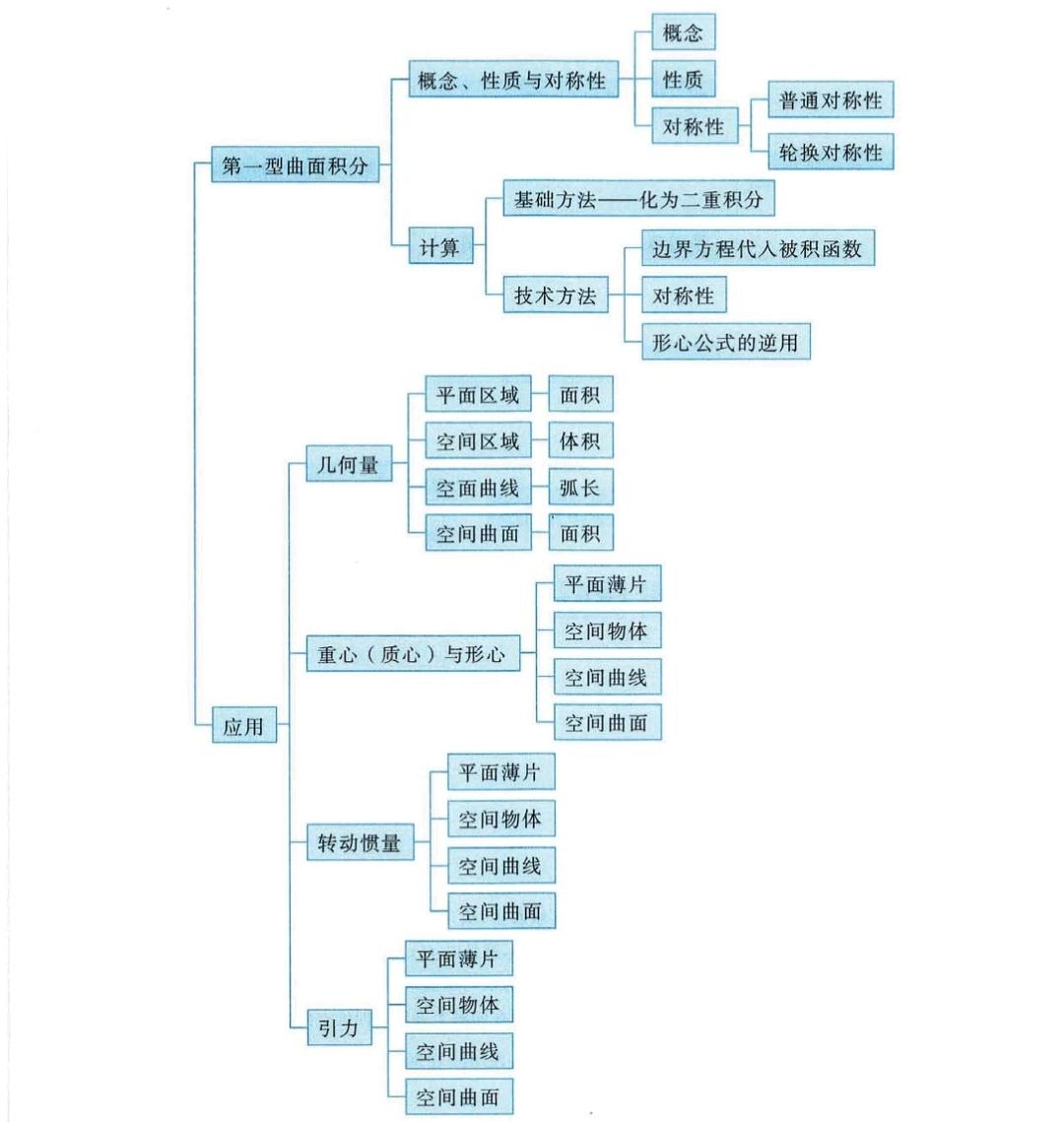
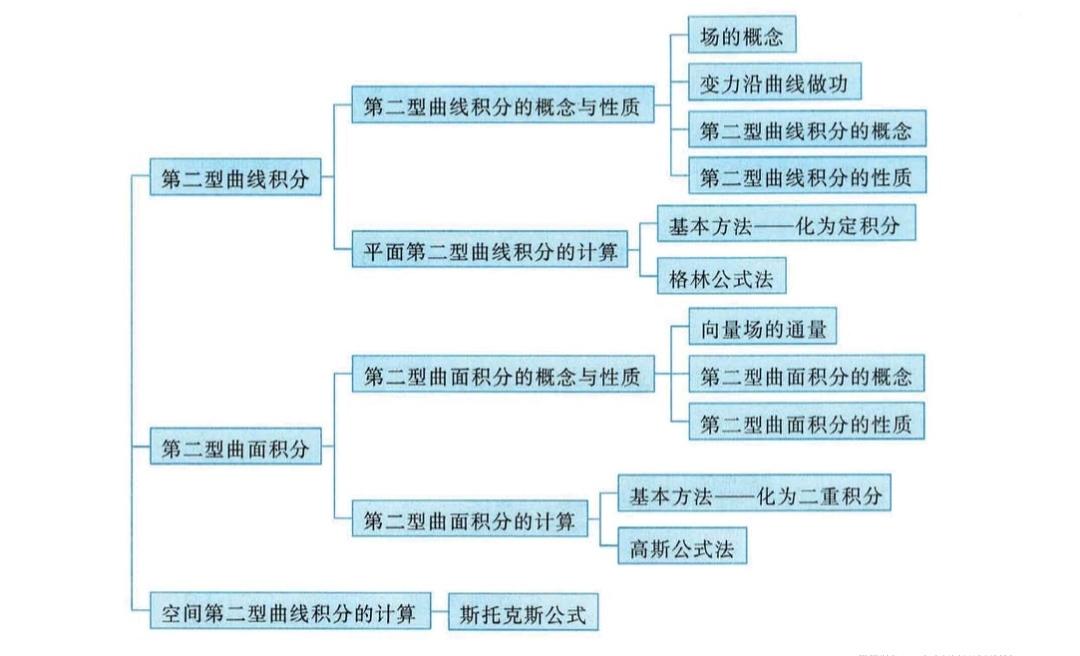
第18章 三重积分+曲线、曲面积分

这一讲的概念跟物理结合很紧密。

第一型的曲线、曲面积分都可以看作是求密度为f的曲线、曲面质量，第二型的曲线、曲面积分是矢量性的积分。
格林公式有环线的和指向中间的形式，分别从二维向三维推广，就可以得到斯托克斯公式和高斯公式。

格林公式的几何意义.pdf
理解斯托克斯公式.pdf

参考资料：
1、张宇–《考研数学基础30讲》及相关视频
2、知乎马同学高赞答案