还有两天就考试，好耶（哭泣）！开始预习课本了！本篇进行第三章节的重点梳理。第四章第五章来不及写成博客了（继续哭泣）…

第三章 自动控制系统的时域分析

3.1 掌握系统稳定性的充要条件，并能根据劳斯判据判定系统的稳定性。（*）

1892年李普亚诺夫首先提出了稳定性的严格数学定义，根据稳定性的定义（P62），当系统满足以下条件时，系统稳定，此条件时充要的。
$$
\lim_{n \rightarrow \infty}C(t)=0
$$
线性系统稳定的充要条件是：系统特征方程的根（即系统的闭环极点）均为负实数或具有负实部的共轭复数。也就是说，系统的全部闭环极点都在复数平面虚轴的左半部。

劳斯稳定判据：在写成s的多项式形式的标准方程中，实部为正数的根的个数等于劳斯表的第一列元素符号改变的次数。

因此，系统稳定的充要条件是：特征方程的全部系数都是正数，并且劳斯表第一列元素都是正数。

3.2 掌握典型输入信号的时域及频域表达式，并掌握阶跃响应性能指标。（*）

1）典型输入信号：

• 单位阶跃函数

时域表达式：
$$
l(t)=\left{\begin{aligned}1&,t\ge0\0&,t<0\\end{aligned}\right.
$$
拉氏变换：$ L[l(t)]=\frac{1}{s}$

频域表达式：

• 单位斜坡函数

时域表达式：
$$
r(t)=\left{
\begin{aligned}
t&,t\ge0\
0&,t<0\
\end{aligned}
\right.
$$

拉氏变换：$L[t∗l(t)]=\frac{1}{s^2}$

频域表达式：

• 单位抛物线函数（加速度阶跃函数）

时域表达式：
$$
r(t)=\left{
\begin{aligned}
&\frac{1}{2}t^2&,t\ge0\
&0&,t<0\
\end{aligned}
\right.
$$
拉氏变换：$L[\frac{1}{2}t^2∗l(t)]=\frac{1}{s^3}$

频域表达式：

2）阶跃响应性能指标：

• 延迟时间tdtd 指输出第一次达到50%稳态值所需时间
  上升时间trtr 指输出响应第一次到达稳态值的时间
  峰值时间tptp 指输出超过稳态值到达第一个峰值cmaxcmax所需要的时间
  最大超调量σσ% 指输出量的最大值超出稳态值的百分比，即

$$
\sigma=\frac{c_max-c_\infty}{c_\infty}*100
$$

• 调节时间tsts 当阶跃响应曲线到达并不再超出误差带所需最小时间，一般取5%c∞c∞的误差
  振荡次数N 在调节时间内响应曲线偏离稳态值的振荡次数
  稳态误差essess 当时间t趋于无穷大时，系统单位阶跃响应的稳态值与输入量l(t)l(t)之差，即

$$
ess=l−c(\infty)
$$

以上指标中，四个时间反映了系统的快速性，σσ和N反映了平稳性，称为动态性能指标；essess描绘了系统的稳态响应，反映了系统的静态性能，又称为静态性能指标。

3.3 掌握控制系统的动态性能指标求取。重点掌握二阶系统的指标求取，对于高阶系统应掌握主导极点的确定方法。（*）

1）一阶系统的动态指标（P73）

可以归纳为几个步骤：

• 写出闭环传递函数$Φ(s)$，并且与典型形式$Φ(s)=\frac{K}{Ts+1}$对照写出T和K
• 求取输出量$c(t)$，$c(t)$是$C(t)$的拉式反变换，$C(t)=L^{−1}(Φ(s)R(s))$
• $c(t)$可以分解成两个式子，分别代表调节响应$c_t(t)$和稳态响应$c_{ss}(t)$

2）二阶系统的动态指标（P75）

典型形式：$Φ(s)=\frac{K}{T^2S^2+2ξTs+1}$

若K=1，又可以写为$Φ(s)=\frac{w_n^2}{S^2+2ξw_ns+w_n^2}$，式中$w_n=\frac{1}{T}$

当输入信号是单位阶跃函数的时候，$R(s)=\frac{1}{s}$，则
$$
C(s)=Φ((s)R(S)=\frac{w_n^2}{S^2+2ξw_ns+w_n^2}\frac{1}{s}=\frac{1}{s}−\frac{s+2ξw_n}{S^2+2ξw_ns+w_n^2}=C_{ss}(s)+C_t(s)
$$
这里面的ξξ和ωnωn被称为二阶系统的特征参数，经过拉式反变换：
$$
c_{ss}=1;c(t)=L^{-1}(-\frac{s+2\xi w_n}{s^2+2\xi w_n+s^2})
$$
$c_t(t)$的特征方程为其分母，两个特征根为
$$
s_{1,2}=−ξω_n±ω_n\sqrt{ξ^2−1}
$$
这里面ξ（阻尼系数）的取值不同时间响应曲线有不同的形状：

• $ξ=0$特征方程有一对共轭虚根（零阻尼）-> 无衰减的周期振荡

  $0<ξ<1$ 特征方程有一对共轭复根（欠阻尼）-> 衰减的振荡
  $ξ=1$ 特征方程有一对相等的负实数根（临界阻尼）-> 单调的衰减过程
  $ξ>1$ 特征方程有两个不同的负实数根（过阻尼）-> 两个指数衰减状态的叠加

[需要掌握的公式]

欠阻尼状态，最大超调量σ%完全由阻尼系数ξ决定：$σ=exp(−πξ/\sqrt{1−ξ^2})$

当ξ比较小时，调节时间：$ts≈\frac{3}{ξω_n}$（取Δ=0.05）

阻尼角β公式：$β=arccosξ$

拉氏变换的终值定理：$\lim_{t \rightarrow \infty}f(t)=lim_{s \rightarrow 0}sF(s)$

当闭环传递函数的$K≠0$时，需要算出ξξ的值并查图来获得调整时间：

[带有零点的二阶系统]

影响：一般来说会是系统响应迅速且具有较大的超调量σσ%。零点与一堆共轭复数在复平面上的相对位置决定了零点对阶跃响应的影响。用α=z/(ξωn)α=z/(ξωn)来量化，αα越小，影响程度越大。

规律：有了零点并不会导致时间常数T0T0，但是会增大阻尼系数ξξ，那么就会影响调节时间和最大超调量两个值。

调节时间：$t_s=(3+ln\frac{l}{z})\frac{1}{ξω_n}$

最大超调量，查图3-28（P90）：

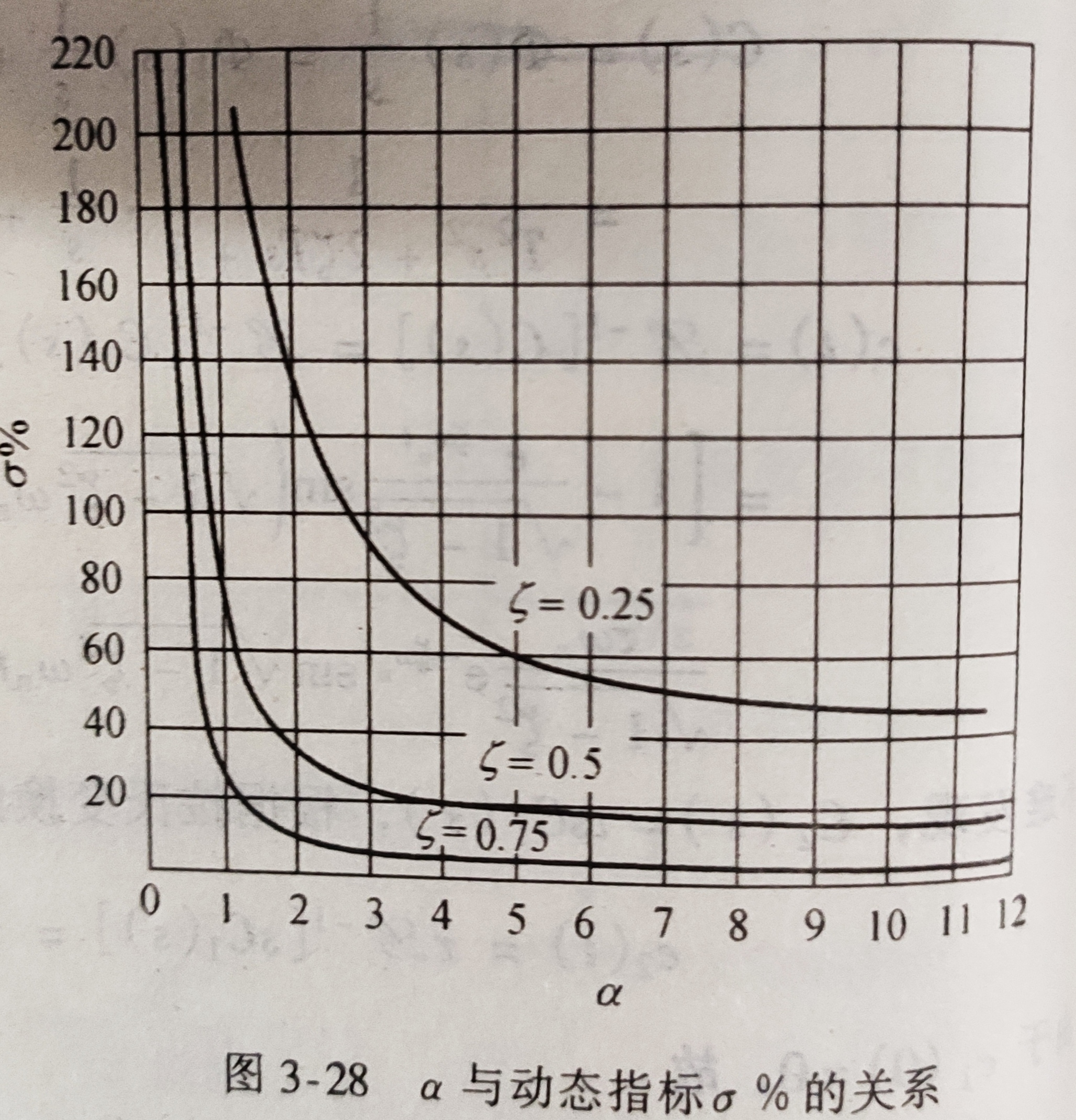
3)高阶系统主导极点的确定方法

闭环主导极点的概念：这一对极点离虚轴最近，并且其他的零极点要么很远要么抵消了。

非主导极点的判定：当引进的实数极点与主导极点的模值之比$α=\frac{p_3}{ω_n}$大于5时，可以认为时非主导极点，影响可以忽略。

3.4 熟悉系统的稳态误差概念，并要求能够求取给定输入作用下及扰动输入作用下稳态误差。（*）

1）稳态误差的定义

• 从输入端定义为稳定时输入信号和反馈信号之差：$e_{ss}=lim_{t→∞}(r(t)−b(t))$
• 从输出端定义为输出量的期望值和实际值之差：$e_{ss}=lim_{t→∞}(c_0(t)−c(t))$
• 由第一种定义推导出来，$e_{ss}=lim_{s→0}\frac{sR(s)}{1+G_K(s)}$

2）工程上根据积分环节的个数υυ对系统进行分类，分别称为0型、Ⅰ型系统、Ⅱ型系统等

3）例题3-19（P109）

3.5 掌握不同系统型别下，系统的静态位置误差系数KpKp、静态速度误差系数KvKv以及静态加速度误差系数KaKa的求取，以及它们与稳态误差的关系。（*）

• 单位阶跃函数输入 $K_p$

与稳态误差的关系$ess=\frac{1}{K_p}$

对0型系统，$K_p=1+K_0$；对于非0型系统，$K_p→∞,e_{ss}=0$

• 单位斜坡函数输入 $K_v$

与稳态误差的关系$ess=\frac{1}{K_v}$

对0型系统，$K_v=0,e_{ss}→∞$；对于Ⅰ型系统，$K_v=K_0,ess=\frac{1}{K_0}$；对于Ⅱ型系统，$K_p→∞,e_{ss}=0$

• 单位抛物线函数输入$K_a$

与稳态误差的关系$ess=\frac{1}{K_a}$

对0型系统，$K_a=0,e_{ss}→∞$；对于Ⅰ型系统，$K_a=0,e_{ss}=→∞$；对于Ⅱ型系统，$K_a=K_0,ess=\frac{1}{K_0}$

表3-6（P105）完美概括：

3.6 了解PID控制器各部分的作用，并能根据实际系统需求选取合适、经济的控制器。

PID调节器各部分的作用分别是比例(P)、积分(I)、微分(D)控制算法。

比例，反应系统的基本（当前）偏差，系数大，可以加快调节，减小误差，但过大的比例使系统稳定性下降，甚至造成系统不稳定；

积分，反应系统的累计偏差 ，使系统消除稳态误差，提高无差度，因为有误差，积分调节就进行，直至无误差；

微分，反映系统偏差信号的变化率，具有预见性，能预见偏差变化的趋势，产生超前的控制作用，在偏差还没有形成之前，已被微分调节作用消除，因此可以改善系统的动态性能。但是微分对噪声干扰有放大作用，加强微分对系统抗干扰不利。

参考资料：

1、自动控制原理（第四版，高国燊等人著）

2、PID调节器各部分的作用分别是什么？