本次实验将要通过根轨迹来分析系统性能。

本篇文章记录自动控制原理的后三个实验，包括“基于MATLAB控制系统的根轨迹及其性能分析”，“基于MATLAB控制系统的Nyquist图及其稳定性分析”和“基于MATLAB控制系统的Bode图及其频域分析”。

$4. 基于MATLAB控制系统的根轨迹及其性能分析

1、实验目的

（1）熟练掌握使用MATLAB绘制系统零极点图和根轨迹图的方法；

（2）学会分析控制系统根轨迹的一般规律。

（3）利用根轨迹图进行系统性能分析。

2、开环闭环传递函数

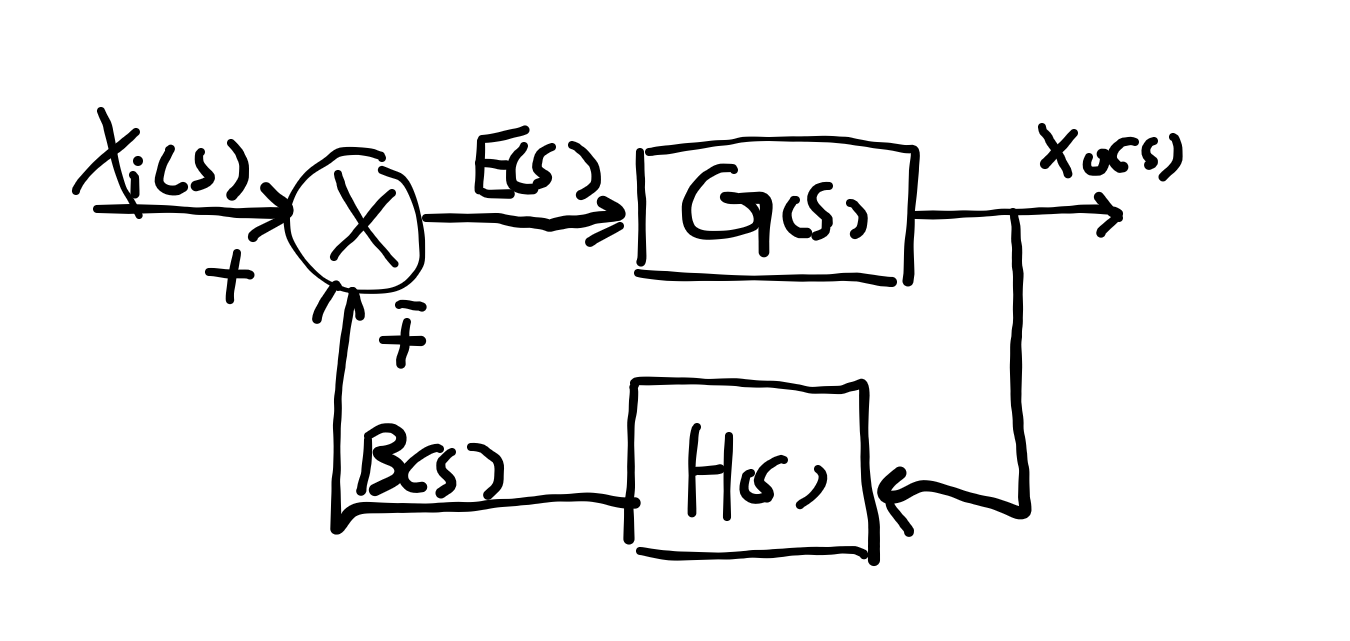
G(s)称为前向通道传递函数，是输出Xo(s)与偏差E(s)之比；

H(s)称为反馈回路传递函数，是反馈信号B(s)与输出Xo(s)之比；

而G(s)*H(s)是被人为定义为系统的开环传递函数Gk(s)，也是反馈信号与偏差之比；

闭环传递函数的定义则为输出与输入之比。

3、根轨迹

3.1 概念

根轨迹是开环系统某一参数从零变到无穷时，闭环系统特征方程式的根在s平面上变化的轨迹。根轨迹是分析和设计线性定常控制系统的图解方法，使用十分简便，特别在进行多回路系统的分析时，应用根轨迹法比用其他方法更为方便，因此在工程实践中获得了广泛应用。

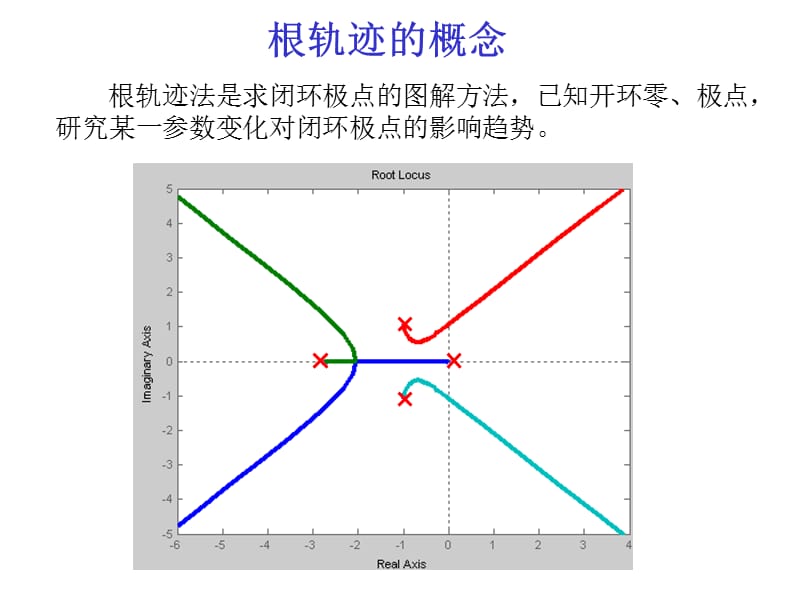
3.2 根轨迹与系统稳定性

1.如果根轨迹全部位于s平面左侧，就表示无论增益怎么改变，特征根全部具有负实部，则系统就是稳定的。

2.如果根轨迹在虚轴上，表示临界稳定，也就是不断振荡。

3.如果根轨迹根轨迹全部都在s右半平面，则表示无论选择什么参数，系统都是不稳定的。

也就是说增益在一定范围内变化时，系统可以保持稳定，但是当增益的变化超过这一阈值时，系统就会变得不稳定，而这一阈值就是出现在根轨迹与虚轴的交点上，在这一点系统临界稳定。最终可由增益的取值范围判断系统的稳定性。

3.3 绘制法则

根轨迹的绘制具有以下绘制法则：

法则1.起点和终点

根轨迹的起点和终点。根轨迹起于开环极点（包括无限极点），终于开环零点（包括无限零点）。

法则2.分支数、对称性和连续性

根轨迹的分支数、对称性和连续性。根轨迹的分支数与开环有限零点数m和有限极点数n中的大者相等，它们是连续的并且对称于实轴。

法则3.渐近线

根轨迹的渐近线。当开环n>m时，有n-m条根轨迹分支沿着与实轴交角为$\varphi_a$、交点为$\sigma_a$的一组渐近线趋向无穷远处，且有$\varphi_a=\frac{(2k+1)\pi}{n=m}(k=0,1,2,…,n-m-1)$和$\sigma_a=\frac{\sum_{i=1}^{n}p_i-\sum_{j=1}^{m}}{n-m}$

法则4.在实轴上的分布

根轨迹在实轴上的分布。实轴上的某一区域，若其右边开环实数零、极点个数之和为奇数，则该区域必是根轨迹。

法则5.分离点与分离角

根轨迹的分离点与分离角。两条或两条以上根轨迹分支在s平面上相遇又立即分开的点，称为根轨迹的分离点，分离点的坐标d是下列方程的解：
$$
\sum_{j=1}^m\frac{1}{d-z_j}=\sum_{i=1}^m\frac{1}{d-p_i}
$$

式中，$z_j$为各开环零点的数值；$p_i$为各开环极点的数值；分离角为$(2k+1)\pi/l$

法则6.起始角与终止角

根轨迹的起始角与终止角。根轨迹离开开环复数极点处的切线与正实轴的夹角，称为起始角；根轨迹进入开环复数零点处的切线与正实轴的夹角，称为终止角。这些角度都可以由特定关系式求出。

法则7.与虚轴的交点

根轨迹与虚轴的交点。若根轨迹与虚轴相交，则交点上的$K’$值和$\omega$值可用劳斯判据确定，也可令闭环特征方程中的$s=j\omega$，然后分别令其实部和虚部为零而求得。

法则8.根之和

根之和。
$$
\sum_{i=1}^ns_i=\sum_{i=1}^np_i
$$

3.4 实验例子

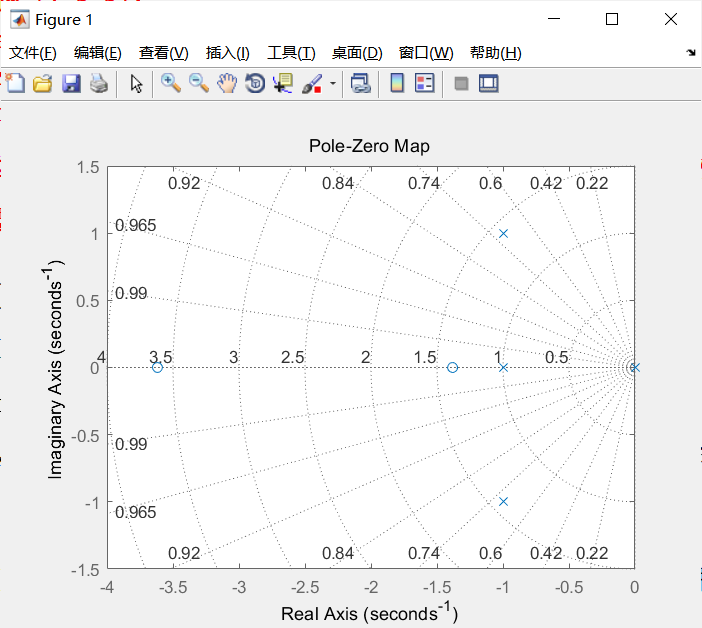
1. 已知系统的开环传递函数为$G_k(s)=\frac{s^2+5s+5}{s(s+1)(s^2+2s+2)}$，绘制系统的零极点图

num=[1 5 5];den=[1 3 4 2 0];pzmap(num,den);grid;

2）已知系统的开环传递函数为$G_k(s)=\frac{k}{s(s+1)(s+2)}$，绘制控制图系统的根轨迹图，并分析根轨迹的一般规律

num=[1];den=[1 3 2 0];rlocus(num,den);grid

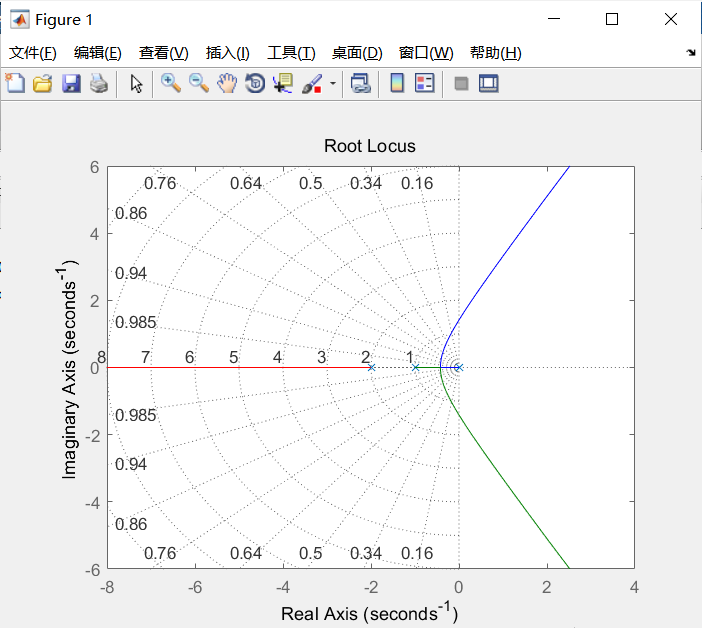
根轨迹的一般规律：[黑人问号.jpg]

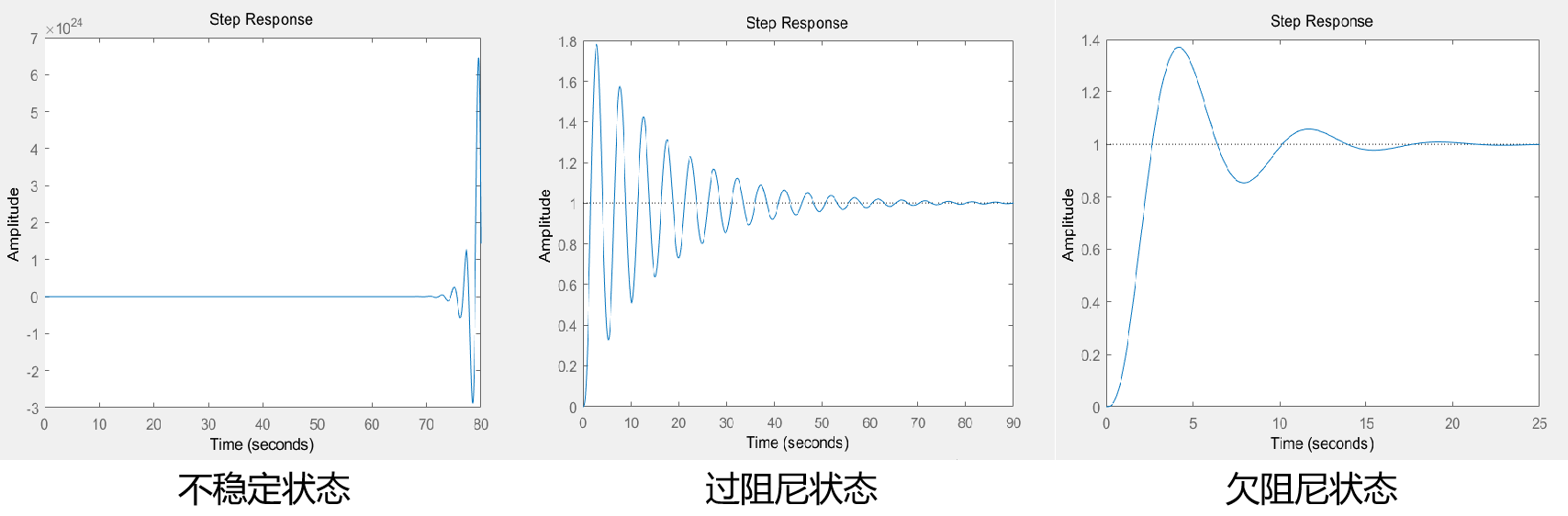
3）在实验内容（2）中控制系统的根轨迹上分区段取点，构造闭环系统传递函数，分别绘制其对应的阶跃响应曲线，并比较分析

k=1;z=[];p=[0 -1 -2];[num,den]=zp2tf(z,p,k);rlocus(num,den);grid[k,r]=rlocfind(num,den)[num,den]=zp2tf(z,r,k);step(num,den)

• s轴右侧 -> 不稳定状态
• s轴左侧的曲线弯头部分，产生一对共轭复根 -> 欠阻尼状态
• 曲线零点处，产生两个相同的特征根 -> 临界稳定状态
• 左边线段处，特征根均为负实数 -> 过阻尼状态

参考资料：

1、百度百科：根轨迹

2、开环传递函数与闭环传递函数区别？

$5. 基于MATLAB控制系统的Nyquist图及其稳定性分析

1、实验目的

（1）熟练掌握使用MATLAB绘制系统Nyquist图的方法；

（2）能够分析控制系统Nyquist图的基本规律；

（3）加深理解控制系统奈奎斯特稳定性判据的实际应用；

（4）学会用奈氏图设计控制系统。

2、概念解释

2.1 幅相频率特性曲线

以角频率$\omega$为参变量，当从$\omega$从$0\to\infty$变化时，频率特性构成的向量在复平面上描绘出的曲线称为幅相频率特性曲线，又称为极坐标图，或Nyquist曲线，简称奈氏图。

一般表达形式，其中$A(\omega)$和$\varphi(\omega)$分别代表了系统的幅频特性和相频特性：
G(jω)=A(ω)ejφ(ω)=A(ω)cos(φ(ω))+j∗A(ω)sin(φ(ω))G(jω)=A(ω)ejφ(ω)=A(ω)cos(φ(ω))+j∗A(ω)sin(φ(ω))

2.2 奈奎斯特稳定性判据（又称奈氏判据）

奈奎斯特稳定性判据是利用系统开环频率特性来判断闭环系统稳定性的一个判据，便于研究当系统结构参数改变时对系统稳定性的影响。其内容是：反馈控制系统稳定的充分必要条件是当$\omega$从$-\infty\to+\infty$时，开环系统的奈氏曲线$G_k(j\omega)$不穿过（-1，j0）点且逆时针包围临界点（-1，j0）的圈数N等于开环传递函数的正实部极点数P。具体地说：

①对于开环稳定的系统，闭环系统稳定的充分必要条件为开环系统的奈氏曲线$G_k(j\omega)$不包围（-1，j0）点。反之闭环系统不稳定。

②对于开环不稳定系统，有P个开环极点位于右半s平面，则闭环系统稳定的充分必要条件为当$\omega$从$-\infty\to+\infty$时，开环系统的奈氏曲线$G_k(j\omega)$逆时针包围（-1，j0）点P次。

重要公式：

• *N = Z - P *
• 当闭环系统稳定时，Z=0，上式可变为N = - P

3、实验内容

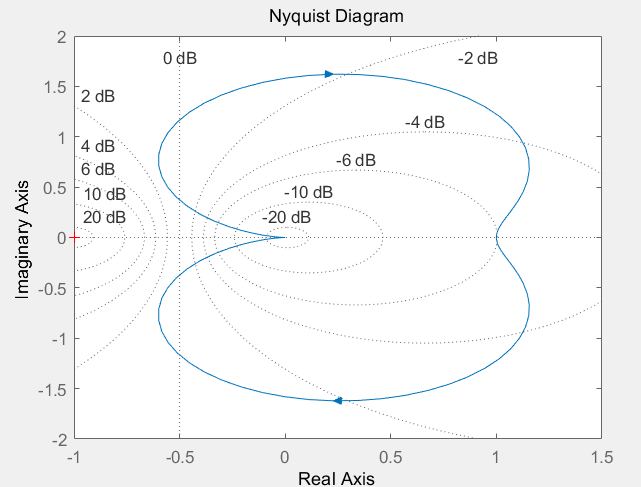
1）已知系统的开环传递函数为$G_k(s)=\frac{10}{s^2+2s+10}$，绘制其Nyquist图

num=10;den=[1 2 10];nyquist(num,den)grid

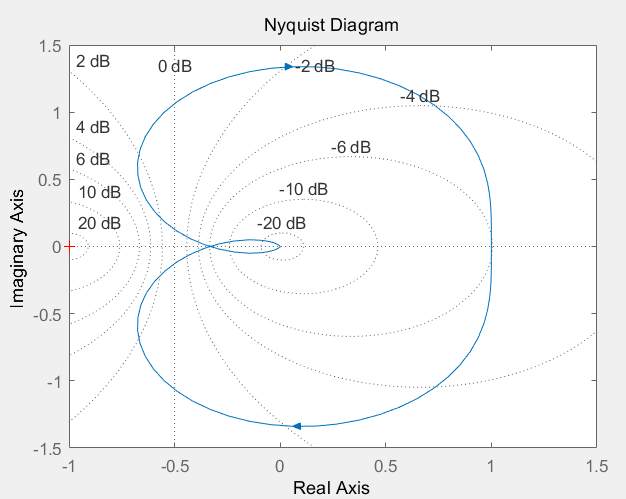
2）已知系统的开环传递函数为$G_k(s)=\frac{0.5}{s^3+2s^2+s+0.5}$，绘制其Nyquist图，并判定系统的稳定性

% 第一步，绘制系统的Nyquist图，相应的程序为：num=0.5;den=[1 2 1 0.5];nyquist(num,den)grid% 第二步，确定开环极点在右半s平面的个数p,相应的程序为p=[1 2 1 0.5];roots(p)

运行结果：s右半平面有3个开环极点，所以P=3。看图可知，N=0。

所以Z=N+P=0+3=3，闭环系统不稳定。

参考内容：

1、欧拉公式

2、百度百科：奈奎斯特稳定判据

$6. 基于MATLAB控制系统的Bode图及其频域分析

1、实验目的

（1）熟练掌握运用MATLAB命令绘制控制系统Bode图的方法；

（2）了解系统Bode图的一般规律及其频域指标的获取方法；

（3）熟练掌握运用Bode图分析控制系统稳定性的方法。

2、相关概念

2.1 对数频率特性曲线

又称频率特性的对数坐标图或伯德（Bode）图，由对数幅频特性曲线（纵坐标为$10lg|G_k(j\omega)|$，单位是分贝，dB）和对数相频特性曲线（纵坐标为度，°）组成，两者的横坐标都是角频率$\omega$，采用$lg(\omega)$分度。

用对数频率特性曲线表示系统频率特性的优点是：

①幅频特性的乘除运算转变为加减运算；

②对系统作近似分析时，只需画出对数幅频特性曲线的渐近线，大大简化了图形的绘制；

③可以用实验方法将测得的系统（或环节）频率响应的数据画在半对数坐标纸上，根据所做出的曲线，估计被测系统的传递函数。

2.2 对数稳定判据

对数频率特性曲线是奈氏判据移植到对数频率坐标的结果。若$G_k(j\omega)$包围（-1，j0）点，即$G_k(j\omega)$在点（-1，j0）左边有交点，在Bode图中表现为$L(\omega)>0$分贝所在的频段范围内，$\varphi(\omega)$与-180°线有交点。

对数频率稳定性的判据为：闭环系统稳定的充分必要条件是当$\omega$从零变化到$+\infty$时，在开环系统对数幅频特性曲线$L(\omega)>0$分贝的频段内，相频特性$\varphi(\omega)$穿越$(2k+1)\pi(k=0,\pm1,\pm2,…)$的次数N为$\frac{P}{2}$，其中$N=N_+-N_-$，$N_+$为正穿越次数，$N_-$为负穿越次数，P为开环传递函数的正实部极点数。

2.3 稳定裕度

1）相角裕度$\gamma$

2）幅值裕度$h_g$

3）关于相角裕度和增益裕度的几点说明：控制系统的相角裕度和幅值裕度是系统幅相特性曲线对（-1，j0）点靠近程度的度量。因此，这两个裕度可以用来作为设计准则。只用幅值裕度或相角裕度都不足以说明系统的相对稳定性，必须同时给出这两个量。

对于最小相位系统，只有当相角裕度和幅值裕度都是正值时系统才是稳定的。负的裕度表示系统不稳定。为了得到满意的性能，相角裕度应当在30°-60°之间，幅值裕度应大于6dB。