近期即将迎来自动控制原理的考试，考前要做六个实验，遂写下两篇文章为记。

本篇记录前三个实验，包括“时域分析法”，“Simulink仿真”，“用Matlab实现几种典型信号时间响应”。

$1. 时域分析实验

1、实验目的：

1、观察单位阶跃信号输入时二阶系统的时间响应，分析ξ、Wn对响应曲线及瞬态响应指标tn tp ts Mp%的影响。

2、了解二阶系统瞬态响应指标的意义其计算。

---

2、实验内容

2.1 将系统的零极点增益模型转换成传递函数模型

G(s)=6(s+3)(s+1)(s+2)(s+5)G(s)=6(s+3)(s+1)(s+2)(s+5)

k=6z=[-3]p=[-1,-2,-5][num,den]=zp2tf(z,p,k);

2.2 对典型二阶系统G(s)=ω2s2+2ξωns+ω2nG(s)=ω2s2+2ξωns+ωn2输入单位阶跃信号1（t）,且wn=1，ξ分别等于-0.1；-0.2；0；0.1；0.5；1；1.5。及ξ=0.5，wn分别等于1; 10; 30; 50的响应曲线。

wn=1kosi=[0 , 0.1 , 0.5 , 1 , 1.5]figure(1)hold onfor kos=kosinum=[ wn ^ 2];den=[1 , 2*kos* wn , wn^ 2];step(num,den)endtitle('Step Response')hold offgridzoom on

---

3、遇到问题：

3.1matlab中，zp2tf()函数

作用：将系统函数的零极点形式 (zp) 转化为系统函数一般形式 (tf) 的系数。

在这里2应该代表转换；zp，zero point & pole -> 零极点；tf, transfer function -> 传递函数。

在matlab中，有一个函数tf(?)，是传递函数的意思，一般学自动控制原理的时候经常用，在s域中，比如要输入G（s）=1/（s^2+2s+1），就可以在matlab中输入G=tf（[1],[1 2 1]）。

零极点形式：分子式系数为k，零点从分子产生（z1, z2, …），极点从分母中产生（p1, p2, …）。

举栗：得到了系统函数H(s)的零极点的值，z为零点的值，p为极点的值，k为系数，如图所示，n1为a的值，d1为b的值，这里的n1,d1,z,p均为向量形式。

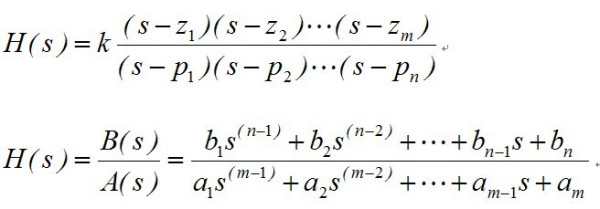
3.2 matlab中，step()函数

官方注释
Step response plot of dynamic system; step response data

官方Description

step calculates the step response of a dynamic system. For the state-space case, zero initial state is assumed. When it is invoked with no output arguments, this function plots the step response on the screen.

作用：将一个动态系统的阶跃响应绘图

3.3 matlab中，tf()函数

官方注释

Transfer function model

官方Description

Use tf to create real-valued or complex-valued transfer function models, or to convert dynamic system models to transfer function form.

Transfer functions are a frequency-domain representation of linear time-invariant systems. For instance, consider a continuous-time SISO dynamic system represented by the transfer function sys(s) = N(s)/D(s), where s = jw and N(s) and D(s) are called the numerator and denominator polynomials, respectively. The tf model object can represent SISO or MIMO transfer functions in continuous time or discrete time.

---

4、知识整理

4.1 Z变换

Z变换（英文：z-transformation）可将时域信号（即：离散时间序列）变换为在复频域的表达式。它在离散时间信号处理中的地位，如同拉普拉斯变换在连续时间信号处理中的地位。离散时间信号的Z变换是分析线性时不变离散时间系统问题的重要工具，在数字信号处理、计算机控制系统等领域有着广泛的应用。

Z变换在离散系统中的地位与作用，类似于连续系统中的拉氏变换 。同时具有许多重要的特性：如线性、时移性、微分性、序列卷积特性和复卷积定理等等。

已有现成的与拉氏变换表类似的Z表。对于一般的信号序列，均可以由表上直接查出其Z变换。相应地，当然也可由信号序列的Z变换查出原信号序列，从而使求取信号序列的Z变换较为简便易行。

4.2 系统函数

用单位脉冲响应h(n)可以表示线性时不变离散系统，这时 y（n）=x（n）*h（n） 两边取z变换：**Y(z)=X(z)H(z)**则定义为系统函数。

定义：

系统函数是个具有实系数的复变量S的有理函数，即实有理函数，所以它的极点和零点或者是实数而位于实轴上，或者是成共轭对的复数而位于与实轴对称的位量上。就是说，系统函数的极点和零点的分布必定对实轴成镜像对称。

常用系统：因果系统、稳定系统、因果稳定系统

极点和零点：

• 系统函数的极点和零点的分布必定对实轴成镜像对称。

• 系统函数一般有n个有限的极点和m个有限的零点。

  如果n>m，则当s为无穷大时。函数值
  limx→∞H(s)=limx→∞bmsmansnlimx→∞H(s)=limx→∞bmsmansn
  为零，所以H(s)在无穷大处有一个（n-m）阶的零点，零极点个数都是n个；如果n<m，则当s为无穷大时，函数值
  limx→∞H(s)=limx→∞bmsmansnlimx→∞H(s)=limx→∞bmsmansn
  亦为无穷大，所以H(s)在无穷大处有一个（m-n）阶的极点，零极点个数都是m个。

  根据函数分子和分母幂次的高低，可以有若干零点在无穷大处，或者若干极点在无穷大处，即从广义上来说，系统函数极点和零点的数目应该相等。(看不懂)

  

4.3 线性时不变系统

两方面，一方面是线性，满足叠加原理；另一方面是时不变特性。

时不变系统的定义：

就是系统的参数不随时间而变化，即不管输入信号作用的时间先后，输出信号响应的形状均相同，仅是从出现的时间不同。

用数学表示为T[x(n)]=y[n]则 T[x(n-n0)]=y[n-n0]，这说明序列x(n)先移位后进行变换与它先进行变换后再移位是等效的。

4.4 单位脉冲响应

介绍：单位脉冲响应(Unit impulse response)系统对单位脉冲输入的响应。也称作记忆函数。脉冲响应确定一个线性系统的特性，包含有与频率域中的传输函数相同的信息，而传输函数是脉冲响应的拉普拉斯变换。线性系统的输出由系统的输入与它的脉冲响应的卷积给出。

含义： 单位脉冲响应是指一个无穷大的瞬时冲激，并且由于其在时间轴上的积分为1，而t又趋向于零，所以单位脉冲响应的大小应该是无穷大，但是要知道的是，无穷大量也有大小比较，所以单位脉冲响应可以用一个系数对之进行量度。

场景： 在数字信号处理中，单位脉冲响应代表系统的性质，是描述系统的数学公式，也是系统的数学模型。例如：当系统的初始状态为零时，这时给系统输入一个单位脉冲序列x(n)=δ(n)，则系统的输出称为单位脉冲响应，简称脉冲响应，用符号h(n)表示。
δ(n)={1(当n=0时)0(当n≠0时)δ(n)={1(当n=0时)0(当n≠0时)

参考资料：

1、[n1,d1]=zp2tf(z,p,k)在matlab中什么意思

2、matlab里面的tf函数是什么怎么用

3、MATLAB中的step()函数

4、百度百科：Z变换

5、百度文库：第六章 系统函数3-4

6、百度百科： 线性时不变系统

7、百度百科：单位脉冲响应

$2. Simulink仿真

实验内容：

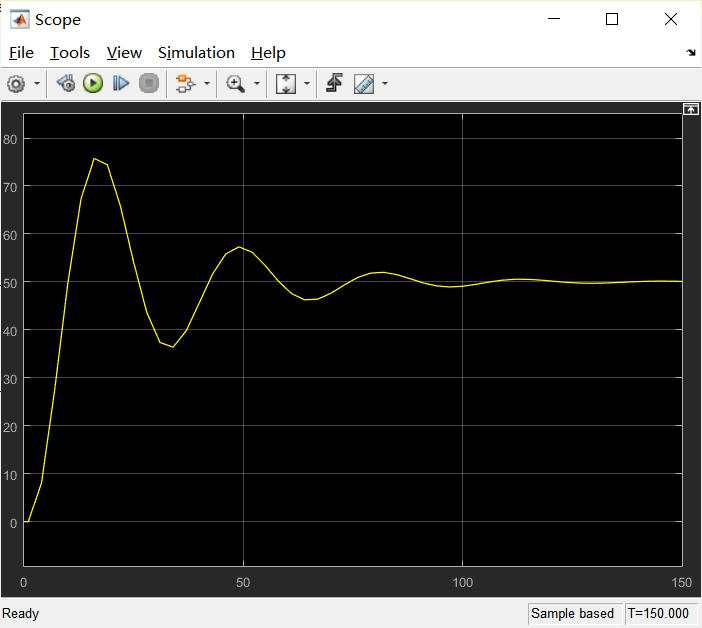
用Matlab仿真（simulink）图示系统输入单位阶跃信号1(t)的响应，分析响应曲线的稳态响应Xoss(t),振荡频率wd(rad/s)最大超调量Mp,峰值时间tp,进入稳态值+5%误差带的调整时间ts。

---

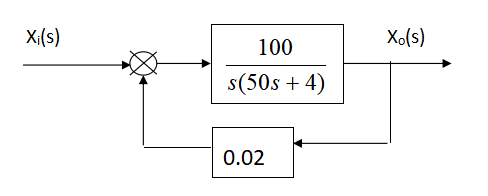
实践过程

1、进入matlab的simulink进行控件的排布和拖放

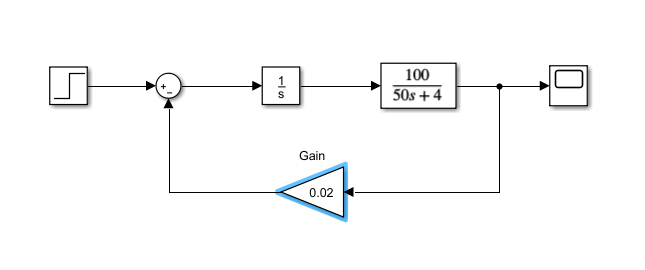
2、调整时间

3、得出结果图

参考资料：

1、MATLAB使用Simulink 进行建模与仿真方法

$3. 用Matlab实现几种典型信号时间响应

1、实验内容

掌握在matlab环境下建立控制系统模型的方法，并学会调用相应的函数实现单位脉冲信号，单位阶跃信号和单位斜坡信号的响应；

2、典型信号时间响应

2.1 单位阶跃响应

• 单位阶跃函数

单位阶跃函数（Unit Step Function）属于典型输入信号，是一种狄利克雷函数，其形式如下：
u(x)={0,t<01,t>0u(x)={0,t<01,t>0
很明显的一点是，单位阶跃函数在t=0这一点是不连续的。

• 零状态响应

所谓零状态响应是指系统在接收到指定输入之前处于初始状态，即保证系统是完全因为指定输入（在此为单位阶跃输入）而产生的响应变化。

• 单位阶跃响应

  单位阶跃响应，就是指系统在接收到单位阶跃函数输入后产生的零状态响应。

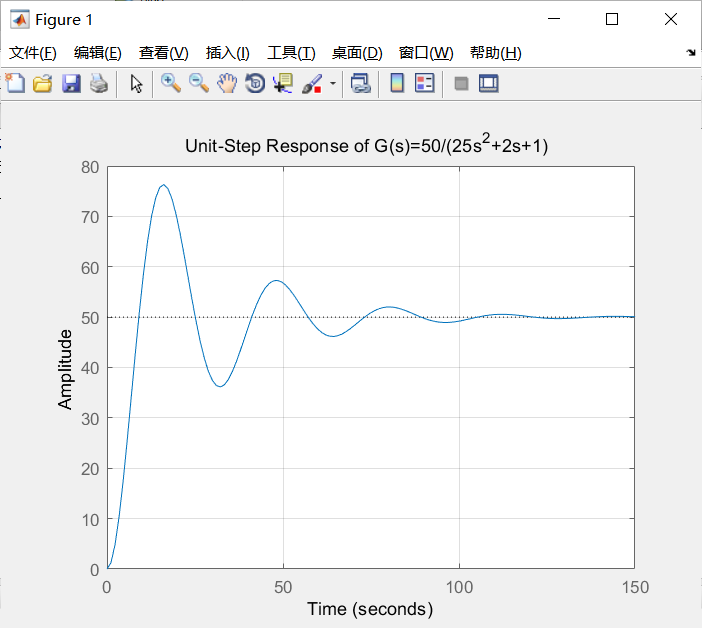
• 作用和意义

a) 系统动态性能分析

动态性能是系统性能的一个十分重要的指标，通常用阶跃信号作用来测定系统的动态性能。

一般认为，阶跃信号对于系统来说是十分严峻的工作状态，因为阶跃信号中存在跃断点（不连续点）。

针对零初始状态系统在单位阶跃输入下的响应情况，定义了一系列动态性能指标，用以评判系统的动态性能，如超调量、衰减比、上升时间、调节时间、峰值时间等等。

b) 建立系统响应模型

对于典型的输入信号，如冲激信号、阶跃信号、斜坡信号等，都建立有响应模型（在此即单位阶跃响应模型）。根据模型，可以快速判断出实际系统的动态性能指标参数，只需要代入实际系统的相关测量参数，就可以定量分析其性能指标。

2.2 单位脉冲响应

• 单位脉冲函数

单位脉冲序列δ(n)的数学定义是
δ={0t≠0∞t=0δ={0t≠0∞t=0
而脉冲的面积，即冲量为单位1
S=∫+∞−∞δ(t)dt=1S=∫−∞+∞δ(t)dt=1

• 脉冲响应函数

在信号与系统或电路理论等学科中，冲激响应(或叫脉冲响应)一般是指系统在输入为单位冲激函数时的输出（响应）。对于连续时间系统来说，冲激响应一般用函数h(t)来表示。对于无随机噪声的确定性线性系统，当输入信号为一脉冲函数 δ（t） 时，系统的输出响应 h（t）称为脉冲响应函数。

脉冲响应函数可作为系统特性的时域描述。 至此，系统特性在时域可以用h(t)来描述，在频域可以用H(ω)来描述，在复数域可以用H(s) 来描述。三者的关系也是一一对应的。

对于任意的输入 u（t）， 线性系统的输出 y（t）表示为脉冲响应函数与输入的卷积， 即如果系统是物理可实现的,那么输入开始之前，输出为0，即当 τ<0时 h(τ)=0，这里τ 是积分变量。

• 卷积

简单定义：卷积是分析数学中一种重要的运算。

设:f(x),g(x)是R1上的两个可积函数，作积分：
∫+∞−∞f(τ)g(x−τ)dt∫−∞+∞f(τ)g(x−τ)dt
可以证明，关于几乎所有的实数x，上述积分是存在的。这样，随着x的不同取值，这个积分就定义了一个新函数h(x)，称为函数f与g的卷积，记为*h(x)=(f*g)(x)*。

• 单位脉冲响应

  单位脉冲响应，就是指系统在接收到单位脉冲函数输入后产生的零状态响应。

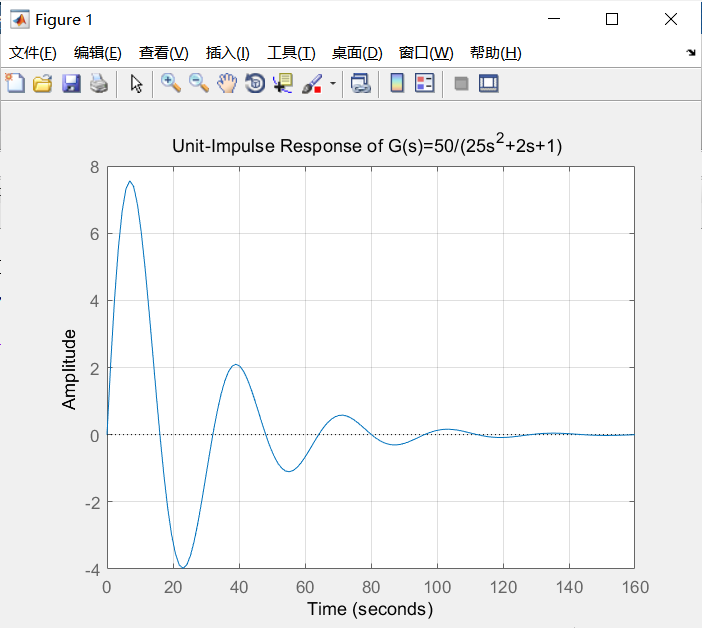
2.3 单位斜坡响应

• 斜坡函数

  斜坡函数是一元实函数，因其图像像斜坡而得名。斜坡函数在负半轴函数值为零，正半轴为形如y=At的正比例函数。A=1时，称为单位斜坡函数。斜坡函数是系统动力学中经常用来研究系统模型及其反馈系统的有关信息的测试函数。 其函数表达式为：
  r(t)=max(0,t)r(t)=max(0,t)

• 单位斜坡响应

  单位斜坡响应，就是指系统在接收到单位斜坡函数输入后产生的零状态响应。

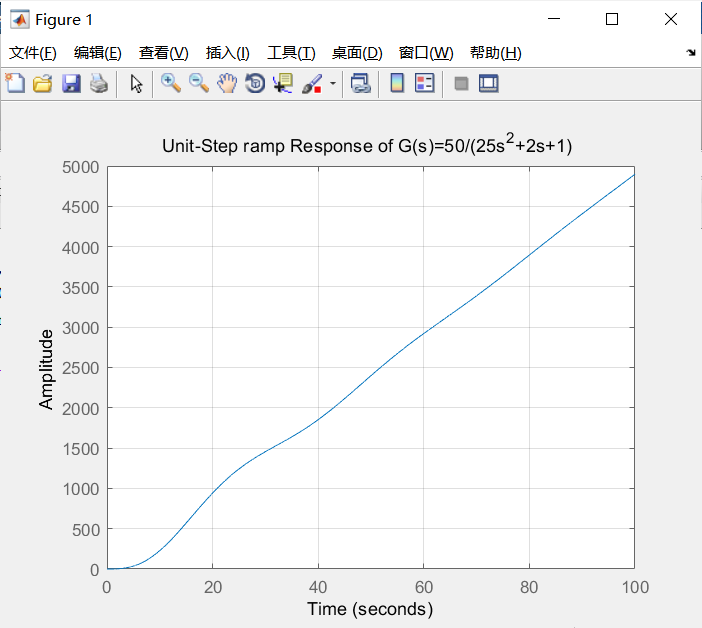
3、问题

Q：Matlab中没有斜坡响应信号对应的函数，为什么能用阶跃信号来求解？

A：因为斜坡响应信号的一阶导数就是阶跃信号，四种典型信号的关系如下：

参考资料：

1、百度百科：单位阶跃响应

2、自动控制原理（第四版，高国燊等人著）

3、单位阶跃响应单位斜坡响应

4、[小技巧]让Hexo在使用Mathjax时支持多行公式